Dych chi wedi edrych allan trwy’r ffenest erioed, gan feddwl tybed sut bydd y tywydd heddiw? Datganai rhagolygon y tywydd gydag argyhoeddiad y noson gynt byddai hi mor braf â’r haf yn yr Aifft. Ond erbyn hyn, mae hi’n bwrw glaw, ac yn edrych fel petai corwynt o Kansas yn cyrchu tuag at eich cartref. Wrth gwrs, ychydig o orliwiad yw hyn, ond serch hynny mae’r cwestiwn yn codi: beth sy’n bod ar yr holl ymdrechion i ddisgrifio a deall y fath hon o ffenomen ffisegol? Mae Patrick yn esbonio mwy…
Have you ever looked out through the window, thinking, I wonder what the weather will be like today? The weather forecast declared with conviction the night before that it would be a stifling as summer in the Sahara. But by now, it’s raining, and looking as if a hurricane from Kansas is heading for your homestead. Of course, this is a bit of an exaggeration, but despite that the question arises: what’s up with all our efforts to describe and understand this kind of physical phenomenon? Patrick explains more…
| 1. Ein Byd Dyrys? Yn anffodus, mae’r anhawster yn rhan anhepgorol o’r peth sy’n cael ei archwilio. Mae’n codi’n naturiol pan fydd unrhyw system yn cynnwys rhannau sy’n gallu rhyngweithio gyda'i gilydd gan newid y system ei hun. Hyd yn oed tasai rhywun yn ceisio mesur popeth, a gwyddai’r hafaliadau priodol i gyd, ni fedrai hi ddweud yn gymwys beth fyddai’n dod i fod yn y dyfodol. Y rheswm dros hyn ydy fod yn y byd go iawn, bydd yn amhosibl dilyn trywydd popeth sy’n digwydd ar yr un pryd. Hefyd, ni fydd yn bosibl mesur unrhyw beth â manwl cywirdeb. Ac eto i gyd, y gwahaniaethau lleiaf un eiliad all achosi newidiadau ysgubol yn ddiweddarach. | 1. Our Confusing World? Unfortunately, the difficulty is an inseparable part of the thing that’s being investigated. It arises naturally when any system contains parts that can interact with each other so changing the system itself. Even if someone were to try and measure something, and were to know all the appropriate equations as well, she could not say exactly what would come to pass in the future. The reason for this is that in the real world, it’s impossible to keep track of everything that’s happening at the same time. Also, it’s never possible to measure anything totally accurately. And then again, the smallest differences one second can cause sweeping changes later. |
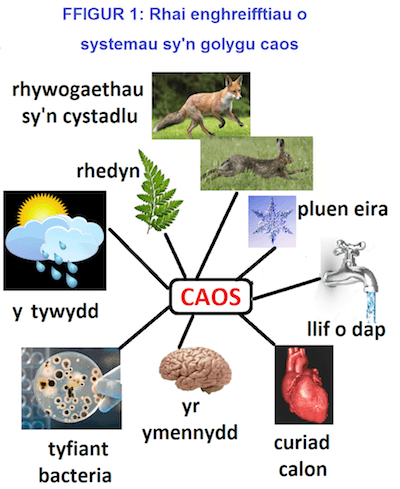
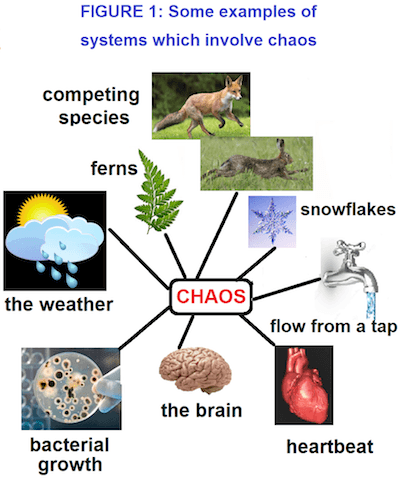
| Dyma’r ffenomen a enwir yn ‘caos.’ Mae caos ym mhob man, drwy’r amser (gweler Ffigur 1). | This is the phenomenon called ‘chaos’. Chaos is everywhere, all the time (see Figure 1). |
|
|
| Efallai y byddai’n ymddangos mai hollol anrhagweladwy yn y bôn yw’r ddaear gron, felly. Ond, wedi dweud hynny, dyw popeth wedi’i golli, oherwydd, ar y llaw arall, fe fydd yr un fath o batrymau cyffredinol i’w weld drwy’r amser, er gwaethaf sut bydd y manylion yn wahanol mewn pob achos. Mewn geiriau eraill, bydd yn amhosibl rhagweld y manylion i gyd bob amser, ond yn aml iawn fe fydd yn bosibl gweld braslun o beth sydd i ddod yn y dyfodol. | Perhaps it would appear that the entire world is basically totally unpredictable, then. But, having said that, all is not lost, because, on the other hand, the same kind of general patterns are to be seen all the time, despite how the details differ in each case. In other words, it’s impossible to predict all the details every time, but very often it will be possible to see a sketch of what is to come in the future. |
| Felly mewn gwirionedd, nid enghreifftiau o anhrefn lwyr ydy’r effeithiau sy’n codi o gaos. Yn hytrach, maen nhw’n gasgliadau o wybodaeth gymhleth, rydym ni’n gallu eu deall, os edrychwn ni arnyn nhw’n gywir. Gadewch i ni archwilio ymhellach. | So in truth, the effects that arise from chaos are not examples of total disorder. Rather, they are collections of complex information, which we can understand, if we look at them correctly. Let’s investigate further. |
| 2. Sefyllfa Syml Dychmygwch facteria’n tyfu mewn dysgl Petri â chlawr, sy’n cynnwys cyflenwad di-ben-draw o fwyd (ie, gallu dychmygu rhai pethau rhyfedd y mae mathemategwyr, hefyd!). Wrth reswm, wrth iddynt fwydo a thyfu, maen nhw’n cynhyrchu gwenwynau sy’n tueddu i’w lladd nhw, ac arafu eu tyfiant. I ddechrau, maint penodedig o facteria sydd yn y ddysgl. Nodwedd hanfodol gyntaf y model yw hwn. | 2. A Simple Situation Imagine some bacteria growing in a covered Petri dish, which contains an endless supply of food (yes, mathematicians can imagine strange things too!). Of course as they feed and grow, they produce poisons which tend to kill them, and slow down their growth. To start, there is a fixed number of bacteria in the dish. This is the first essential characteristic of the model. |
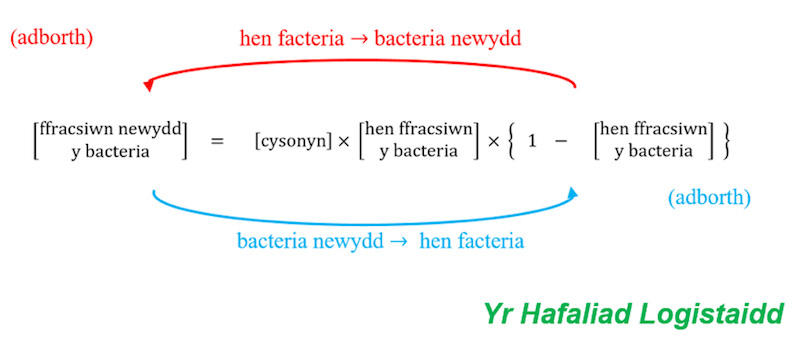
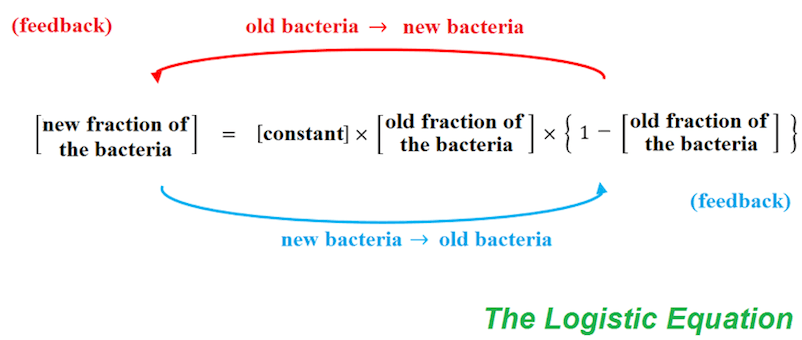
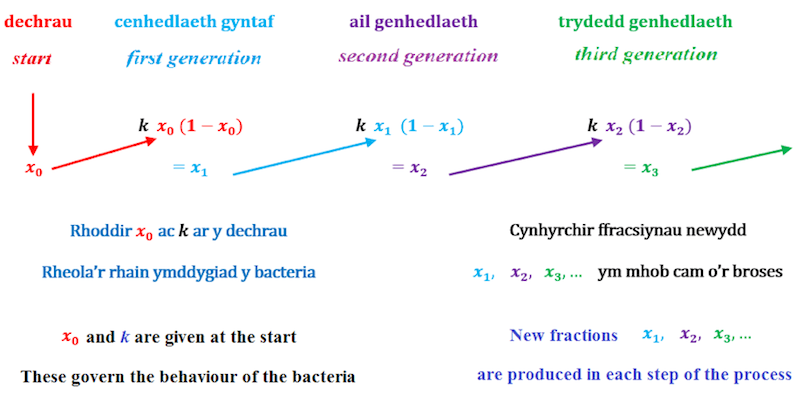
| Sut bydd nifer y bacteria’n newid dros amser? Rydym ni’n gallu defnyddio model mathemategol seml yma. ‘Yr Hafaliad Logistaidd’ ydy ei henw, ond peidiwch â phoeni, dyw hi ddim mor frawychus fel y mae’n swnio! A bod yn onest, haws ydy sôn am ffracsiwn y ddysgl sy’n cynnwys bacteria (yn hytrach na nifer y bacteria), a dyna y byddwn ni’n ei wneud. Mae’r hafaliad yn cynnwys ‘adborth’ achos bydd ffracsiwn newydd y bacteria’n dibynnu ar hen ffracsiwn y bacteria, ac felly bydd y proses yn mynd ymlaen, gan greu cenhedlaeth ar ôl cenhedlaeth | How will the number of the bacteria change over time? We can use a simple mathematical model here. Its name is ‘The Logistic Equation’, but don’t worry, it’s not as frightening as it sounds! To be honest, it’s easier to talk about the fraction of the dish containing bacteria (rather than the number of the bacteria), and that’s what we’ll do. The equation contains ‘feedback’ because the new fraction of the bacteria depends on the old fraction of the bacteria, and so the process goes on, creating generation after generation. |
|
|
| Hollbwysig yw’r ‘cysonyn’, sef nifer sy’n gallu bod rhwng 0 a 4. Mae’n cynrychioli pa mor gyflym bydd y bacteria’n tyfu. Ail nodwedd hanfodol y model yw hwn. | The ‘constant’ is critical, that is a number which can be between 0 and 4. It represents how quickly the bacteria grow. This is the second essential characteristic of the model. |
| 3. Cyfrif Caos Mae’r Hafaliad Logistaidd yn gweithio fel hyn. Cynrychiolir y cysonyn gan k a ffracsiwn y bacteria i gychwyn gan x0: | 3. Calculating Chaos The Logistic Equation works like this. The constant is represented by k and the starting fraction of the bacteria by x0: |
|
|
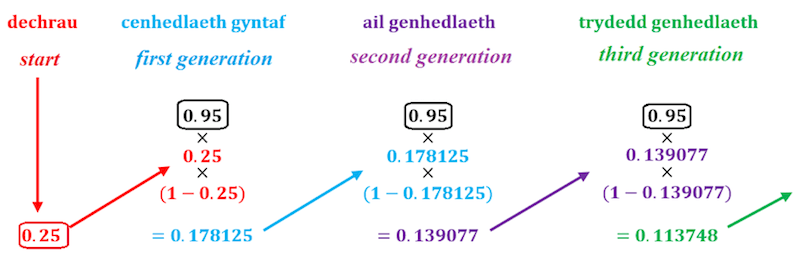
| Dyw’r cyfrifiadau ddim yn anodd eu gwneud ar gyfrifiannell boced. Ystyriwch, er enghraifft, k = 0.95 ac x0 = 0.25: | The calculations aren’t hard to do on a pocket calculator. Consider, for example, k = 0.95 and x0 = 0.25: |
|
|
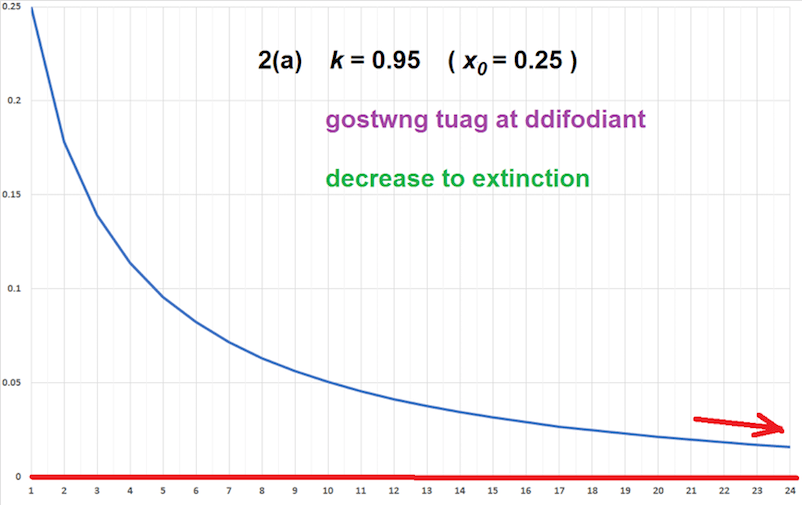
| Mae’n edrych fel petai’r ffracsiynau’n gostwng bob tro. Dangosir graff o’r canlyniadau yn Ffigur 2(a) isod. | It looks as if the fraction is decreasing every time. The graph of the results is shown in Figure 2(a) below. |
| Nesaf, gallwn ni archwilio pum sefyllfa ychwanegol lle mae x0 = 0.25, gan ystyried un enrhif gwahanol o k ym mhob un. Dangosir graffiau o’r canlyniadau yn Ffigurau 2(b) – 2(dd) isod. | Next, we can investigate five additional situations where x0 = 0.25, considering one different value of k in each one. Graphs of the results are shown in Figures 2(b) – 2(dd) below. |
| 4. O Drefn i Gaos Ffigur 2(a) isod (k = 0.95): Dyw’r bacteria ddim yn tyfu, ac mae’r ffracsiwn ohonyn nhw’n gostwng tuag at ddim, hynny yw, maen nhw’n trengi’n llwyr. Dyma ddifodiant. | 4. From Order to Chaos Figure 2(a) below (k = 0.95): The bacteria don’t grow, and the fraction of them decreases towards nothing, that is they die off completely. This is extinction. |
|
|
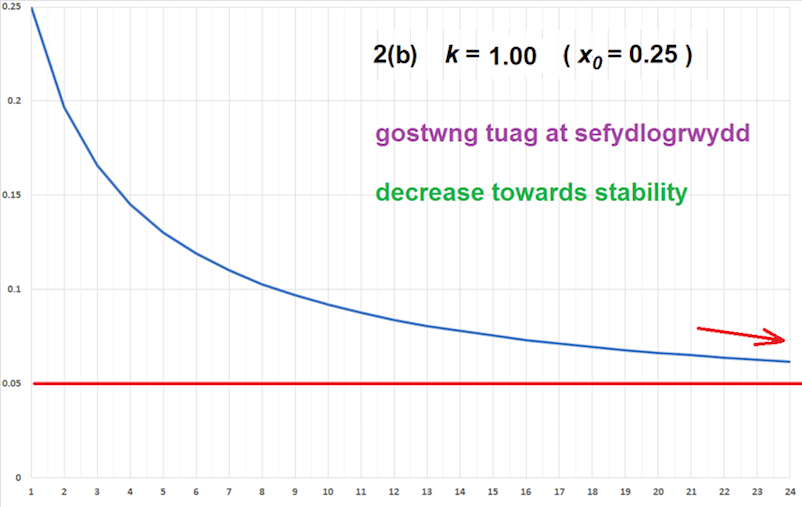
| Ffigur 2(b) isod (k = 1): Mae’r bacteria’n gallu defnyddio’r bwyd i ryw fesur. Dydyn nhw ddim yn dod i ben, ond mae’r ffracsiwn ohonyn nhw’n gostwng tuag at enrhif cyson. Dyma sefydlogrwydd. | Figure 2(b) below (k = 1): The bacteria can use the food to some degree. They don’t disappear, but the fraction of the decreases towards a constant value. This is stability. |
|
|
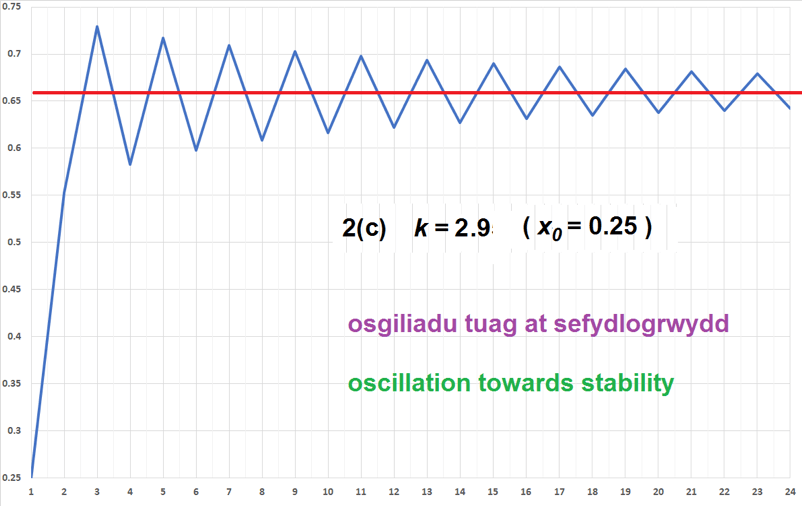
| Ffigur 2(c) isod (k = 2.9): Mae’r bacteria’n gallu defnyddio’r bwyd yn dda. Maen nhw’n tyfu, ond pan fydd gormod ohonynt, byddant yn dechrau marw. Ar ôl hynny, byddan nhw’n gallu tyfu unwaith eto. Yn y pendraw, wedi osgiladu yn ôl ac ymlaen, bydd ffracsiwn y bacteria yn cyrraedd enrhif cyson. Dyma osgiladu tuag at sefydlogrwydd. | Figure 2(c) below (k = 2.9): The bacteria can use the food well. They grow, but when there are too many of them, they begin to die. After that, they can grow once again. In the end, after oscillating back and forth, the fraction of the bacteria will reach a constant value. This is oscillation towards stability. |
|
|
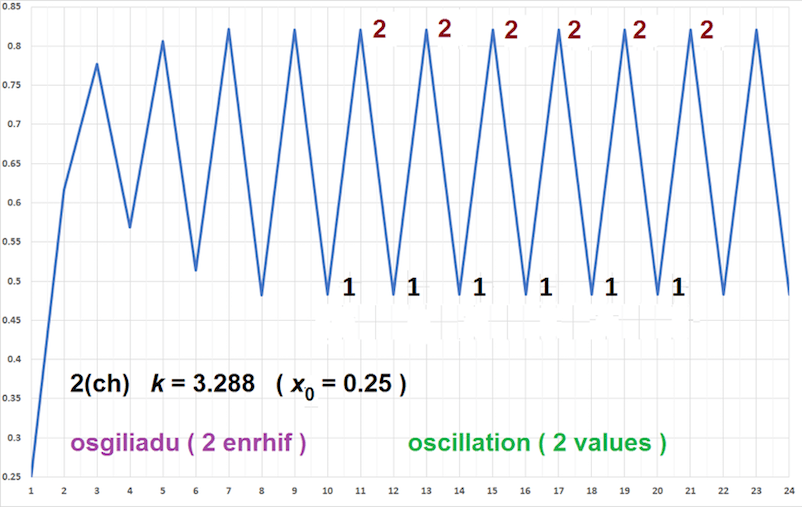
| Ffigur 2(ch) isod (k = 3.228): Mae’r osgiladu’n fwy amlwg. Dydy ffracsiwn y bacteria byth yn cyrraedd enrhif cyson. Maen nhw’n goroesi gan osgiladu rhwng dwy boblogaeth sefydlog. | Figure 2(ch) below (k = 3.228): The oscillations are more obvious. The fraction of the bacteria never reaches a constant value. They survive, oscillating between two stable populations. |
|
|
| Ffigur 2(d) isod (k = 3.506): Mae’r bacteria’n goroesi gan osgiladu rhwng pedair poblogaeth sefydlog. | Figure 2(d) below (k = 3.506): The bacteria survive, oscillating between four stable populations. |
|
|
| Ffigur 2(dd) isod (k = 3.948), llinell las: Mae’r bacteria’n goroesi gan osgiladu’n wyllt. Mae’n ymddangos nad yw unrhyw drefn i’r ffracsiynau. Beth fydd yn digwydd i’r bacteria yn nes ymlaen? Dych chi ddim yn gallu dweud, heb gyfrifo. | Figure 2(dd) below (k = 3.948), blue line: The bacteria survive, but oscillating wildly. It appears that there is no order to the fractions. What will happen to the bacteria later on? You can’t say, without calculating. |
|
|
| Ymhellach, hyd yn oed os bydd ffracsiwn y bacteria’n dechrau o ddau enrhif sy’n agos iawn at ei gilydd, bydd yr ymddygiad yn hollol wahanol mewn cenedlaethau hwyrach. Mae’r enghraifft uchod yn Ffigur 2(dd) hefyd yn ystyried x0 = 0.251 (llinell goch). Edrychwch ar y ddwy linell yn y llun. Maen nhw’n debyg i’w gilydd yn gyntaf oll, ond maen nhw’n dod yn hollol wahanol yn gyflym iawn. | Furthermore, even if the fraction of the bacteria starts from two different values that are very close to each other, the behaviour will be totally different in later generations. The example above in Figure 2(dd) also considers x0 = 0.251 (red line). Look at the two lines in the picture. They are similar to each other first of all, but they become totally different very quickly. |
| Felly, newidiadau bychain yn yr enrhif cychwynnol (er enghraifft) sy’n gallu peri newidiadau aruthrol yn hwyr neu'n hwyrach. Beth fydd yn digwydd i’r bacteria yn y naill achos neu'r llall? Dych chi ddim yn gallu dweud, heb gyfrifo. Yr 'Effaith glöyn byw’ yw’r enw ar yr ymddygiad hwn. Mae’n ein hatgoffa sut mae rhywbeth cyn lleied â chwifio adenydd pili-pala yn Kansas yn gallu newid y tywydd yng Nghymru. | So, small changes in the starting value (for example) can cause extraordinary changes sooner or later. What will happen to the bacteria in one case or the other. You can’t tell, without calculating. ‘The Butterfly Effect’ is the name for this behaviour. It reminds us how something as small as the flutter of a butterfly’s wings in Kansas can change the weather in Wales! |
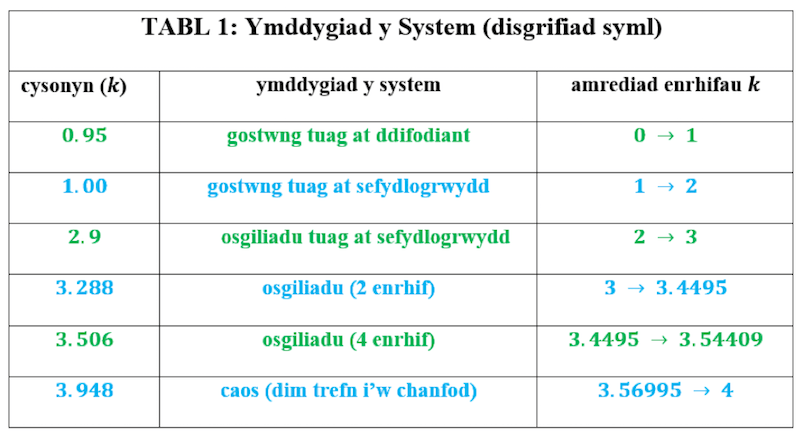
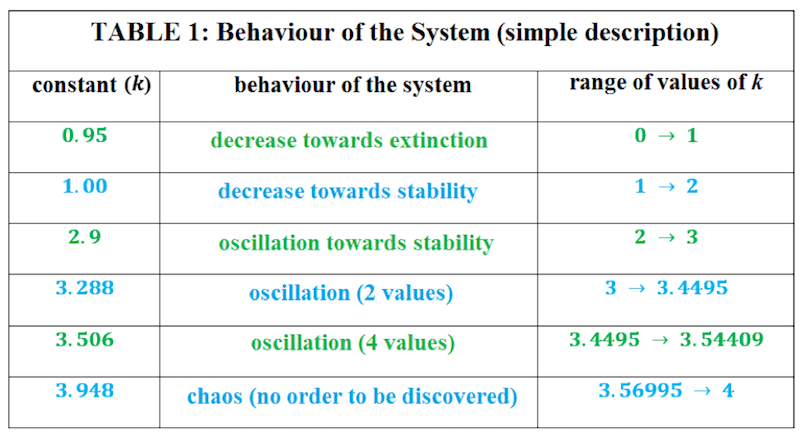
| 5. Trefn ‘Gaotig’ Dyma’r ffenomen o’r enw caos. Pan fydd rhannau unrhyw system yn rhyngweithio gyda’i gilydd, llawer o batrymau gwahanol a all digwydd. Pa un sy’n digwydd a fydd yn dibynnu ar enrhifau a ddisgrifia nodweddion y system, fel tymheredd, pwysau, cyfradd genedigaethau, ac ati. Yn ein henghraifft seml, dim ond dau beth sy’n rheoli ymddygiad y system: enrhif y cysonyn, a ffracsiwn cychwynnol y bacteria. Gall ymddygiad y system ddod i ben yn llwyr, cyrraedd sefydlogrwydd, osgiladu rhwng sawl enrhif, neu newid heb unrhyw batrwm o gwbl (ceir crynodeb yn Nhabl 1). | 5. ‘Chaotic’ Order This is the phenomenon called chaos. When parts of any system interact with each other, there are many different patterns that can occur. Which one happens will depend on values that describe characteristics of the system, like temperature, pressure, birth rates, and so on. In our simple example, there are only two things which control the system’s behaviour: the value of the constant, and the initial fraction of the bacteria. The behaviour of the system can end completely, reach stability, oscillate between several values, or change without any pattern at all (a summary is given in Table 1). |
|
|
| Mae’r ymddygiadau hyn i gyd yn wynebau caos: a’r anhrefn lwyr a’r drefn amlwg. Dan lawer o amgylchiadau bydd system benodol yn ymddwyn yn rheolaidd iawn. Ond llwybr gwastad sydd rhwng trefn ac anhrefn, a reolir gan baramedrau’r system. Mewn system gaotig, y newidiad lleiaf ar un adeg sy’n gallu achosi gwahaniaethau enfawr yn nes ymlaen. Nid y cyfrifon sydd ar fai. Achos nad ydych chi byth yn gallu mesur nodweddion y system yn fanwl gywir, gall beth y byddwch chi’n ei ddarogan fod yn hollol wahanol i beth fydd yn digwydd mewn realiti, dan amodau caotig. Fodd bynnag, fel arfer, byddwn ni’n gallu deall y fath gyffredinol o ymddygiad yn dda iawn, ac fe fedrwn ni wahaniaethu rhwng yr holl fathau amrywiol. | All of these behaviours are faces of chaos: both the complete disorder, and the obvious order. Under many circumstances a definite system will behave very regularly. But there is a smooth path from order to disorder, which is controlled by the system’s parameters. In a chaotic system, the smallest change at one time can cause enormous differences later on. It’s not the calculations which are at fault. Since you can never measure the system’s characteristics totally accurately, what you predict can be totally different from what happens in reality, under chaotic conditions. However, we can usually understand the general type of behaviour very well, and distinguish between all the different kinds. |
| Felly pan fyddwch yn edrych trwy’r ffenest, ac yn meddwl am y tywydd i ddod, peidiwch â rhoi bai ar y proffwydi tywydd. Yn hytrach, dylech chi wenu, gan gofio’r glöyn byw plagus hwnnw yn Kansas! | So, when you look through the window, and think about the weather to come, don’t blame the weather forecasters. Rather, you should smile, remembering that pesky butterfly in Kansas! |